Funzione di hash

Risultato dei primi quattro byte della funzione hash SHA-1.

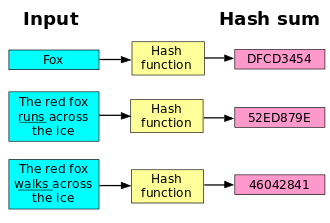
La funzione di hash produce una sequenza di bit (o una stringa), detta digest, strettamente correlata con i dati in ingresso. La parola deriva dal verbo inglese to hash, ovvero sminuzzare, pasticciare, che designa originariamente una polpettina fatta di avanzi di carne e verdure; per estensione, indica un composto eterogeneo cui viene data una forma incerta: "To make a hash of something" vuol dire, infatti, creare confusione, o fare una cosa piuttosto male.

In informatica

Nel linguaggio matematico e informatico, l'hash è una funzione non invertibile che mappa una stringa di lunghezza arbitraria in una stringa di lunghezza predefinita. Esistono numerosi algoritmi che realizzano funzioni hash con particolari proprietà che dipendono dall'applicazione.

Nelle applicazioni crittografiche si chiede, per esempio, che la funzione hash abbia le seguenti proprietà:

• resistenza alla preimmagine: sia computazionalmente intrattabile la ricerca di una stringa in input che dia un hash uguale a un dato hash;
• resistenza alla seconda preimmagine: sia computazionalmente intrattabile la ricerca di una stringa in input che dia un hash uguale a quello di una data stringa;
• resistenza alle collisioni: sia computazionalmente intrattabile la ricerca di una coppia di stringhe in input che diano lo stesso hash.

Nelle applicazioni di basi di dati la funzione hash è usata per realizzare una particolare struttura dati chiamata hash table. In questa applicazione non occorrono proprietà crittografiche e generalmente l'unica proprietà richiesta è che non ci siano hash più probabili di altri.

Hash uniforme semplice

Si definisce hash uniforme semplice quel tipo Hash in cui l'estrazione degli elementi in U è casuale, e la funzione hash

$h:U\to \left\{m\right\}$

estrae la chiave $m_{i}$ con probabilità $1/|m|$

In tali condizioni la ricerca della chiave avrà complessità costante O(1).

Algoritmo di hash

L'algoritmo di hash elabora qualunque mole di bit (in informatica si dice che elabora dati "grezzi"). Si tratta di una famiglia di algoritmi che soddisfa questi requisiti:

1. L'algoritmo restituisce una stringa di numeri e lettere a partire da un qualsiasi flusso di bit di qualsiasi dimensione (può essere un file, ma anche una stringa). L'output è detto digest.
2. L'algoritmo non è invertibile, ossia non è possibile ricostruire il documento originale a partire dalla stringa che viene restituita in output ovvero è una funzione unidirezionale, quest'ultima caratteristica non è indispensabile se si usano gli hash per controllare gli errori nei trasferimenti dei dati, dove le eventuali funzioni di criptaggio possono venir svolte in altre aree del protocollo.

Hash e collisioni

Non esiste una corrispondenza biunivoca tra l'hash e il testo. Dato che i testi possibili, con dimensione finita maggiore dell'hash, sono più degli hash possibili, per il principio dei cassetti ad almeno un hash corrisponderanno più testi possibili. Quando due testi producono lo stesso hash, si parla di collisione, e la qualità di una funzione di hash è misurata direttamente in base alla difficoltà nell'individuare due testi che generino una collisione. Per sconsigliare l'utilizzo di algoritmi di hashing in passato considerati sicuri è stato infatti sufficiente che un singolo gruppo di ricercatori riuscisse a generare una collisione. Questo è quello che è avvenuto ad esempio per gli algoritmi SNEFRU, MD2, MD4, MD5 e SHA-1.

Un hash crittograficamente sicuro non dovrebbe permettere di risalire, in un tempo confrontabile con l'utilizzo dell'hash stesso, ad un testo che possa generarlo.

Applicazioni

Hash e crittografia

La lunghezza dei valori di hash varia a seconda degli algoritmi utilizzati. Il valore più comunemente adottato è di 128 bit, che offre una buona affidabilità in uno spazio relativamente ridotto. Tuttavia va registrata la possibilità d'uso di hash di dimensione maggiore (SHA, ad esempio, può anche fornire stringhe di 224, 256, 384 e 512 bit) e minore (che però è fortemente sconsigliato).

Le funzioni hash svolgono un ruolo essenziale nella crittografia: sono utili per verificare l'integrità di un messaggio, poiché l'esecuzione dell'algoritmo su un testo anche minimamente modificato fornisce un message digest completamente differente rispetto a quello calcolato sul testo originale, rivelando la tentata modifica.

Le funzioni di hash possono essere anche utilizzate per la creazione di firme digitali, in quanto permettono la rapida creazione della firma anche per file di grosse dimensioni, senza richiedere calcoli lunghi e complessi: è infatti computazionalmente più conveniente eseguire con rapidità un hashing del testo da firmare, e poi autenticare solo quello, evitando così l'esecuzione dei complessi algoritmi di crittografia asimmetrica su moli di dati molto grandi.

La firma digitale è definita come il digest di un documento che poi viene crittografato con chiave privata (e non con quella pubblica, come avviene di solito). La firma digitale è l'unico caso in cui l'uso delle chiavi è invertito: la chiave pubblica serve a decrittare la firma e trovare poi il digest iniziale attraverso l'hash, mentre quella privata serve a crittografare una stringa anziché ad aprirla.

Un ulteriore uso delle funzioni di hash si ha nella derivazione di chiavi da password o passphrase: a partire da un valore arbitrario in ingresso (una stringa o un array di larghe dimensioni) si deriva in modo crittograficamente sicuro (ovvero non è possibile abbreviare il calcolo con una qualche scorciatoia) una chiave di dimensioni adatte alla cifratura. È appena il caso di dire, tuttavia, che a meno di prendere debite contromisure (come l'uso di un salt crittografico), l'utilità di questa procedura è esclusivamente pratica: infatti la sicurezza della chiave derivata è equivalente a quella della stringa di ingresso ai fini di un attacco a dizionario. Di contro, è certamente più comodo per un essere umano ricordare una stringa piuttosto che una lunga sequenza numerica.

Sicurezza delle funzioni hash

Nel contesto delle funzioni hash, ci si riferisce a diversi concetti di sicurezza:

• Sicurezza debole: dato un messaggio $M$, è computazionalmente "difficile" trovare un secondo messaggio $M'$ tale che $h(M)=h(M')$.
• Sicurezza forte: è computazionalmente "difficile" trovare una coppia di messaggi $M$, $M'$ tali che $h(M)=h(M')$.

Questi due concetti di sicurezza vengono distinti anche per via degli effetti che essi possono produrre nel caso in cui ne siano privi: per quanto riguarda ad esempio la possibilità di effettuare una firma digitale, un algoritmo che non garantisca la sicurezza forte, ma quella debole, sarebbe comunque utile dal momento che il messaggio $M$ non può essere "controllato" e bisognerebbe quindi trovare un secondo messaggio $M'$ con uguale funzione di hash, il che sarebbe appunto computazionalmente difficile.

Hash e basi di dati

È possibile utilizzare le funzioni di hash per creare una hash table, che è una struttura dati molto efficiente per le operazioni di ricerca. La hash table contiene dati associati ad una chiave di ricerca e viene spesso utilizzato nei database per indicizzare gli elementi che saranno oggetto di ricerca. Questa tecnica (detta di hashing) permette di realizzare funzioni di ricerca che riescono ad individuare l'elemento desiderato in un tempo costante, indipendente (almeno in teoria) dal numero di elementi presenti nell'indice.

Protezione dagli errori

L'uso delle funzioni hash per trovare errori nelle trasmissioni è molto comune. La funzione hash viene calcolata dal mittente a partire dai dati e il suo valore è inviato insieme ai dati. Il ricevente calcola di nuovo la funzione hash, e se i valori hash non corrispondono, significa che è avvenuto un errore durante la trasmissione. Questo metodo consente un controllo dell'integrità dei dati migliore della più tradizionale checksum.

Informatica forense

Gli algoritmi di hash, in particolare SHA1 e MD5, sono largamente utilizzati nell'ambito dell'informatica forense per validare e ottenere una 'impronta digitale' dei dati acquisiti, tipicamente le copie forensi. La recente legislazione impone infatti una catena di custodia che permetta di preservare i reperti informatici da eventuali modifiche successive all'acquisizione: tramite i codici hash è possibile in ogni momento verificare che quanto repertato sia rimasto immutato nel tempo. Se i codici hash corrispondono, entrambe le parti in un procedimento giudiziario hanno la ragionevole certezza di lavorare sulla stessa versione dei reperti, garantendo quindi una uniformità di analisi e in genere di risultati. I risultati dei codici hash vengono ormai calcolati di default dalla maggioranza dei software per acquisizione forense e allegati alle copie forensi salvate.

Elenco di hash e documenti correlati

• MD2
• MD4
• MD5
• MDC-2
• SHA-1
• SHA-2 (256, 384, 512)
• RIPEMD-160
• PANAMA
• TIGER
• ADLER32
• HMAC

Voci correlate

• Autenticazione
• Crittografia
• Hash table
• Firma digitale
• Funzione crittografica di hash
• Hashcash
• Rolling hash
• Limite di Bremermann

Altri progetti

Altri progetti

• Wikiversità
• Wikimedia Commons

• Wikiversità contiene risorse sulla funzione di hash
• Wikimedia Commons contiene immagini o altri file sulla funzione di hash

Collegamenti esterni

• (EN) Eric W. Weisstein, Hash Function, su MathWorld, Wolfram Research.
• (EN) Denis Howe, hash function, in Free On-line Dictionary of Computing. Disponibile con licenza GFDL
• (EN) Definizione inglese del termine, su dictionary.cambridge.org. URL consultato il 7 novembre 2005 (archiviato dall'url originale il 13 marzo 2007).
• (EN) Hash'em all!, per calcolare online l'hash di stringhe e file
• Hash Generatore Altro Online Hash Generatore, ha alcune funzioni di hash come md2,md4,md5,sha1,snefru, tiger, haval, ripemd, whirlpool e tra gli altri. Circa 118 differenti algoritmi
• Daniele Frongia e Raffaello Martinelli, Funzioni hash con PHP, su segnalazionit.org, 9 ottobre 2008. URL consultato il 13 ottobre 2022 (archiviato dall'url originale il 23 marzo 2016).
• Programma gratuito per calcolo e verifica hash, su ocr.altervista.org. URL consultato il 15 aprile 2010 (archiviato dall'url originale il 7 maggio 2010).
• Checksums calculator Applicazione gratuita per il calcolo e verifica di funzioni hash per Windows, Linux e Mac OS X.